Você já parou para pensar sobre o número de grãos de areia em todas as praias do mundo? Ou o tamanho de um átomo? Esses números são tão grandes ou tão pequenos que, se tentássemos escrevê-los de maneira convencional, ocupariam páginas e mais páginas. Para lidar com isso de forma prática, os cientistas criaram a notação científica, uma ferramenta que facilita a representação de números extremamente grandes ou pequenos de maneira compacta.

O que é Notação Científica?

A notação científica é uma maneira especial de escrever números usando potências de 10. Ela se divide em duas partes:

1. Um número entre 1 e 10: Esse número representa a magnitude do valor.
2. Uma potência de 10: Indica quantas casas decimais a vírgula deve ser movida para a direita (quando o número é grande) ou para a esquerda (quando o número é pequeno).

Exemplo:
O número 5.000.000 pode ser escrito na notação científica como 5 x 10⁶. Isso significa que a vírgula foi movida 6 casas para a esquerda.

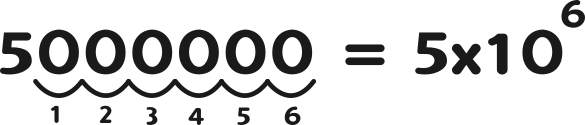
Por que usar a Notação Científica?

• Simplifica a escrita: Números enormes ou muito pequenos se tornam mais fáceis de ler e entender.
• Facilita cálculos: Tornando as operações matemáticas mais rápidas e simples.
• É amplamente usada: Em diversas áreas como Física, Química, Astronomia, e Biologia.

Como funciona na prática?

• Transformando números grandes em notação científica:

1. Identifique a vírgula. Mesmo que não apareça, ela está logo após o último algarismo.
2. Conte as casas decimais que você precisa mover para que o número fique entre 1 e 10.
3. Multiplique o número obtido por 10 elevado ao número de casas decimais.

Exemplo: 32.000.000 = 3,2 x 10⁷

• Transformando números pequenos em notação científica:

1. Identifique a vírgula.
2. Conte as casas decimais que você precisa mover para a direita para que o número fique entre 1 e 10.
3. Multiplique o número obtido por 10 elevado ao número de casas decimais, mas com o sinal negativo.

Exemplo: 0,000005 = 5 x 10⁻⁶

Operações com Notação Científica

• Multiplicação: Multiplica-se os números e soma-se os expoentes das potências de 10.

1. Multiplique os números: Multiplique as partes numéricas (os números que multiplicam as potências de 10).
2. Multiplique as potências de 10: Mantenha a base 10 e some os expoentes.

Exemplo:

(2 x 10³) x (4 x 10⁵)

1. Multiplicamos os números: 2 x 4 = 8
2. Multiplicamos as potências de 10: 10³ x 10⁵ = 10⁸ (somamos os expoentes)

Resultado: 8 x 10⁸

Outro Exemplo:

(5,6 x 10⁻²) x (3 x 10⁴)

1. Multiplicamos os números: 5,6 x 3 = 16,8
2. Multiplicamos as potências de 10: 10⁻² x 10⁴ = 10² (somamos os expoentes)

Resultado: 16,8 x 10²

Atenção: Se o resultado da multiplicação da parte numérica for maior que 10, você precisa ajustar o resultado para que a parte numérica fique entre 1 e 10.

Exemplo:

(7 x 10²) x (6 x 10³) = 42 x 10⁵

Como 42 é maior que 10, podemos reescrever como 4,2 x 10⁶ (movemos a vírgula uma casa para a esquerda e aumentamos o expoente em 1).

• Divisão: Divide-se os números e subtrai-se os expoentes das potências de 10.

1. Divida os números: Divida as partes numéricas (os números que multiplicam as potências de 10).
2. Divida as potências de 10: Mantenha a base 10 e subtraia os expoentes.

Exemplo:

(8 x 10⁵) ÷ (2 x 10³)

1. Dividimos os números: 8 ÷ 2 = 4
2. Dividimos as potências de 10: 10⁵ ÷ 10³ = 10² (subtraímos os expoentes)

Resultado: 4 x 10²

Outro Exemplo:

(6,4 x 10⁻²) ÷ (1,6 x 10⁴)

1. Dividimos os números: 6,4 ÷ 1,6 = 4
2. Dividimos as potências de 10: 10⁻² ÷ 10⁴ = 10⁻⁶ (subtraímos os expoentes)

Resultado: 4 x 10⁻⁶

Ajustando o Resultado:

Assim como na multiplicação, se o resultado da divisão da parte numérica não estiver entre 1 e 10, você precisa ajustar o resultado.

Exemplo:

(9 x 10⁶) ÷ (3 x 10²) = 3 x 10⁴

Aplicações da Notação Científica

A notação científica é amplamente utilizada em várias áreas do conhecimento, como:

• Astronomia: Para representar distâncias imensas entre planetas e estrelas.
• Física: Para expressar valores como a carga do elétron ou a constante de Planck.
• Química: Para representar o número de átomos em uma molécula.
• Biologia: Para descrever o tamanho de microrganismos.

Conclusão

A notação científica é uma ferramenta essencial para quem deseja compreender e lidar com números extremamente grandes ou pequenos. Ao dominar essa técnica, você estará pronto para explorar e realizar cálculos com facilidade em diversos campos do conhecimento.

Gostou deste artigo? Compartilhe com seus amigos e colegas!