Assim como os números, os vetores também podem ser somados, subtraídos e multiplicados por escalares. Vamos explorar cada uma dessas operações com mais detalhes:

Soma de Vetores

A soma de dois ou mais vetores resulta em um vetor chamado vetor resultante. Existem dois métodos principais para somar vetores:

• Método do Triângulo:
  
  1. Desenhe o primeiro vetor (vetor A).
  2. Desenhe o segundo vetor (vetor B), colocando sua origem na extremidade do primeiro vetor.
  3. O vetor resultante (vetor C) é o vetor que liga a origem do primeiro vetor à extremidade do segundo vetor.

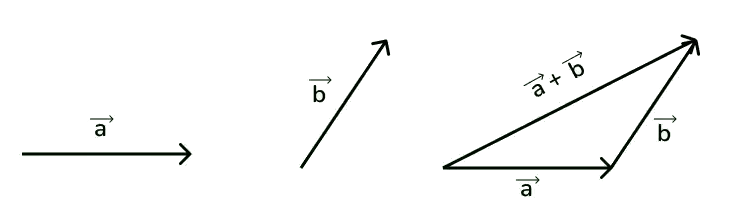
Figura a. Ilustração do método gráfico para adição de vetores: Vetor A é desenhado primeiro, seguido pelo vetor B, cuja origem coincide com a extremidade de A. O vetor resultante C = (A + B) é traçado da origem de A até a extremidade de B.

• Método do Paralelogramo:
  
  1. Desenhe os dois vetores (vetor A e vetor B) com a mesma origem.
  2. Complete o paralelogramo usando os dois vetores como lados.
  3. O vetor resultante (vetor C) é o vetor que liga a origem dos vetores à extremidade oposta do paralelogramo.

Figura b. (a) Vetores P e Q dispostos para soma. (b) Construção do paralelogramo com vetores P e Q, resultando no vetor soma R, que representa a diagonal do paralelogramo.

• Propriedades: 
  • 1) A soma de vetores é comutativa (A + B = B + A)
  • 2) associativa (A + (B + C) = (A + B) + C).

Subtração de Vetores

Subtrair um vetor de outro é equivalente a somar o primeiro vetor com o oposto do segundo vetor. O oposto de um vetor tem a mesma magnitude e direção, mas sentido oposto.

Exemplo: Se temos um vetor A e um vetor B, a subtração A – B é equivalente a A + (-B), onde -B é o oposto do vetor B.

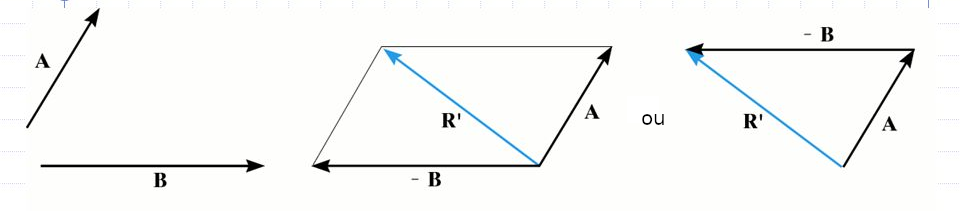
Figura c. Demonstração gráfica da subtração do vetor B do vetor A, utilizando o método do paralelogramo (centro) e o método do triângulo (direita). O vetor resultante R’ é mostrado em ambos os métodos.

Multiplicação por Escalar

Multiplicar um vetor por um escalar (um número real) altera a magnitude do vetor. Se o escalar for positivo, o sentido do vetor não se altera. Se o escalar for negativo, o sentido do vetor é invertido.

Exemplo: Se temos um vetor A e um escalar k:

• Se k > 0, o vetor resultante terá a mesma direção e sentido de A, mas com magnitude k vezes maior.
• Se k < 0, o vetor resultante terá a mesma direção de A, mas sentido oposto e magnitude |k| vezes maior.

Figura d. A imagem ilustra como o vetor v é alterado quando multiplicado por diferentes escalares (2, 1/2 e -1), resultando em vetores com diferentes magnitudes e sentidos.

Exemplo Prático

Imagine um barco atravessando um rio. A velocidade do barco em relação à água é um vetor, e a velocidade da água em relação à margem é outro vetor. A velocidade do barco em relação à margem (velocidade resultante) é a soma vetorial da velocidade do barco em relação à água e da velocidade da água em relação à margem.

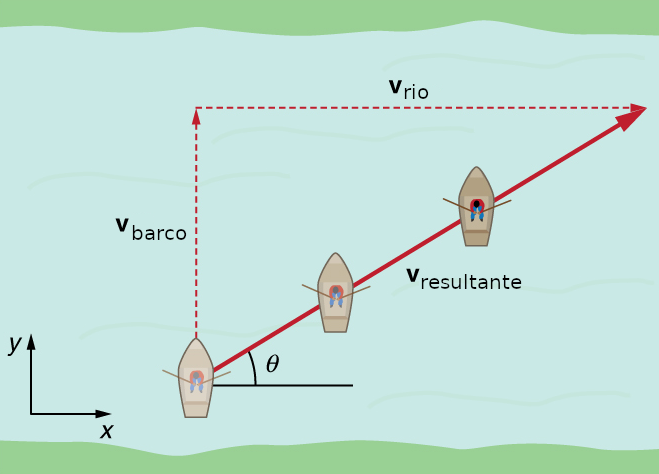
Figura e. Demonstração da soma vetorial da velocidade do barco em relação à água (V_barco) e da velocidade da água em relação à margem (V_rio), resultando na velocidade resultante do barco em relação à margem (V_resultante).