Vetores são grandezas físicas que possuem três características essenciais: módulo (intensidade), direção e sentido. Eles são representados graficamente por setas, onde o comprimento da seta indica o módulo e a direção da seta aponta o sentido.

Figura a. Exemplo de dois vetores.

Exemplos de grandezas vetoriais:

Algumas grandezas que podem ser representadas como vetores incluem força, velocidade, aceleração, deslocamento, campo elétrico e campo magnético.

Figura b. Exemplo de um Diagrama de Forças, onde vetores são usados para representar as características de cada força.

Operações com vetores:

• Adição de vetores: A soma de vetores pode ser feita de forma gráfica (método do paralelogramo – figura c) ou analiticamente, decompondo-os em suas componentes

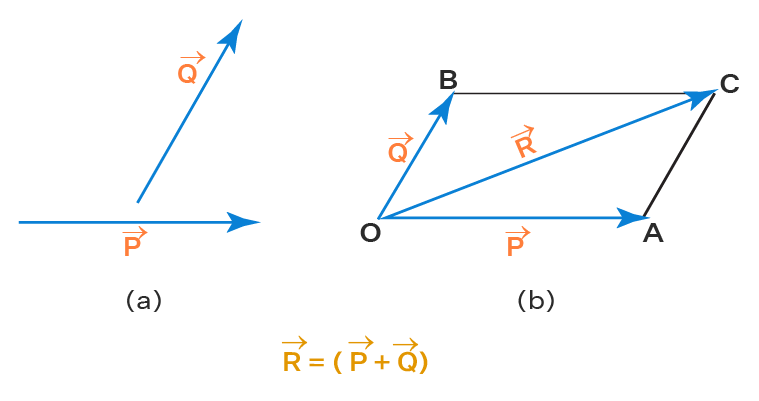
Figura c. Exemplo do uso do Método do Paralelogramo para realizar a adição de dois vetores.

• Subtração de vetores: A subtração de vetores é equivalente à adição do vetor oposto, ou seja, inverte-se a direção do vetor que está sendo subtraído.
• Multiplicação por um escalar: Quando um vetor é multiplicado por um número (escalar), seu módulo é alterado, mas a direção e o sentido permanecem inalterados.

Figura d. Ilustração da multiplicação de um vetor ‘v’ por diferentes escalares, mostrando como o comprimento e a direção do vetor se alteram.

A Importância de Dominar Esses Conceitos

• Descrição precisa dos fenômenos físicos: A linguagem vetorial permite representar de maneira precisa grandezas que possuem direção e sentido, como força e velocidade.
• Resolução de problemas: As operações com vetores são essenciais para resolver problemas em várias áreas da física, como mecânica, eletricidade e magnetismo.
• Compreensão das leis da física: Muitas das leis físicas, como as leis de Newton ou as equações de Maxwell, são formuladas utilizando equações vetoriais, tornando o domínio dos vetores essencial para entender essas leis.

Estudar e entender esses conceitos básicos proporciona as bases necessárias para avançar no estudo da física e resolver os desafios que surgem nas diversas áreas dessa ciência.

Conteúdos do Capítulo

• 2.2 Representação gráfica e algébrica.
• 2.3 Operações básicas: soma, subtração e multiplicação por escalar.
• 2.4 Produto escalar.
• 2.5 Produto vetorial.
• 2.6 Vetores no Espaço e Produto Misto.
• 2.7 Aplicações na geometria analítica: pontos no plano e no espaço, retas e planos.
• 2.8 Aplicações na Física: força, velocidade, aceleração, trabalho, torque e momento angular.