Vetores são entidades matemáticas que possuem tanto magnitude (tamanho) quanto direção. No espaço tridimensional, eles são essenciais para descrever pontos, retas, planos e outras figuras geométricas. O produto misto, por sua vez, é uma operação entre três vetores que fornece informações importantes sobre o volume de um paralelepípedo e a dependência linear entre os vetores.
Vetores no Espaço Tridimensional:
- Definição: Um vetor no espaço tridimensional é representado por um segmento de reta orientado, com um ponto inicial e um ponto final. Ele possui três componentes, correspondentes às coordenadas nos eixos x, y e z.
- Representação: Um vetor v pode ser representado como v = (v₁, v₂, v₃), onde v₁, v₂ e v₃ são as componentes nos eixos x, y e z, respectivamente.
- Operações:
- Adição: A soma de dois vetores u e v é dada por u + v = (u₁ + v₁, u₂ + v₂, u₃ + v₃).
- Multiplicação por escalar: A multiplicação de um vetor v por um escalar k é dada por kv = (kv₁, kv₂, kv₃).
- Produto escalar: O produto escalar de dois vetores u e v é dado por u · v = u₁v₁ + u₂v₂ + u₃v₃. Ele resulta em um escalar e está relacionado ao ângulo entre os vetores.
- Produto vetorial: O produto vetorial de dois vetores u e v é dado por u x v = (u₂v₃ – u₃v₂, u₃v₁ – u₁v₃, u₁v₂ – u₂v₁). Ele resulta em um vetor perpendicular ao plano formado por u e v.
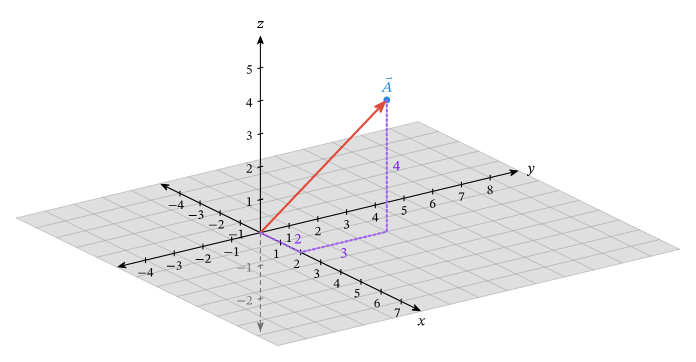
Figura a. A imagem mostra um vetor no espaço tridimensional, com suas componentes representadas nos eixos x, y e z
Produto Misto:
- Definição: O produto misto de três vetores u, v e w é definido como o produto escalar do vetor u com o produto vetorial de v e w: [u, v, w] = u · (v x w).
- Interpretação geométrica: O valor absoluto do produto misto representa o volume do paralelepípedo formado pelos vetores u, v e w.
- Propriedades:
- O produto misto é invariante sob permutações cíclicas dos vetores: [u, v, w] = [v, w, u] = [w, u, v].
- O produto misto muda de sinal sob permutações não cíclicas: [u, v, w] = -[v, u, w] = -[u, w, v] = -[w, v, u].
- Se o produto misto é igual a zero, os vetores são coplanares (estão no mesmo plano).
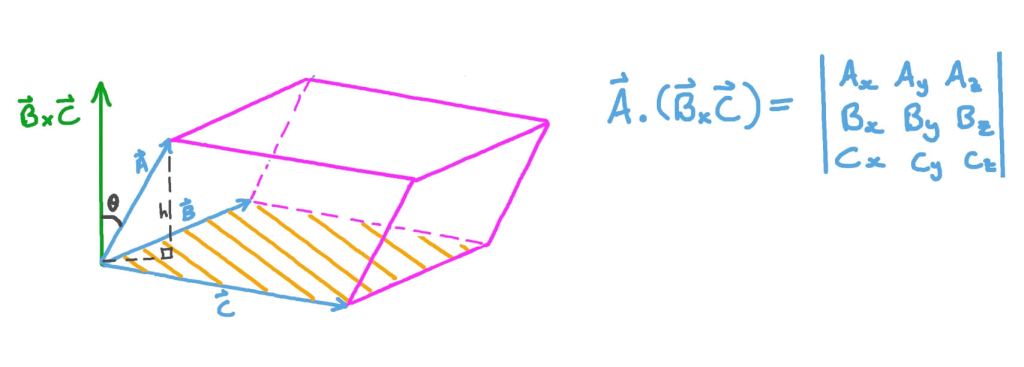
Figura b. Produto misto entre três vetores A, B e C. O resultado do produto misto é um escalar que representa o volume do paralelepípedo formado pelos três vetores
Aplicações:
- Cálculo de volumes: O produto misto é utilizado para calcular o volume de paralelepípedos e tetraedros.
- Verificação de coplanaridade: Se o produto misto de três vetores é zero, eles são coplanares (estão no mesmo plano).
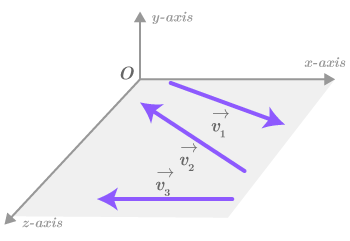
Figura c. A imagem mostra três vetores (v1, v2 e v3) no espaço tridimensional. Os vetores são coplanares, ou seja, estão no mesmo plano (representado pela área sombreada)
- Determinação de dependência linear: Se o produto misto de três vetores é zero, eles são linearmente dependentes.



