O produto vetorial é uma operação entre dois vetores que resulta em um terceiro vetor, perpendicular ao plano formado pelos dois vetores originais. Ele é amplamente utilizado em diversas áreas da física, engenharia e computação gráfica, especialmente em cálculos envolvendo rotações, torques e áreas.  

Definição

Dados dois vetores u e v, o produto vetorial entre eles, denotado por u x v, é definido como um vetor com as seguintes propriedades:

1. Direção: Perpendicular ao plano que contém u e v.
2. Sentido: Dado pela regra da mão direita: se os dedos da mão direita curvam de u para v, o polegar aponta na direção de u x v.
3. Magnitude: |u x v| = |u| |v| sen(θ), onde |u| e |v| são as magnitudes de u e v, respectivamente, e θ é o ângulo entre eles.

Propriedades

O produto vetorial possui as seguintes propriedades:

1. Não comutativo: u x v = – (v x u)
2. Distributivo: u x (v + w) = u x v + u x w
3. Associativo: (αu) x v = α(u x v), onde α é um escalar.
4. Produto vetorial de um vetor por si mesmo: u x u = 0
5. Ortogonalidade: Se u e v são paralelos (o ângulo entre eles é 0° ou 180°), então u x v = 0.
6. Magnitude: A magnitude do produto vetorial |u x v| é igual à área do paralelogramo formado por u e v.

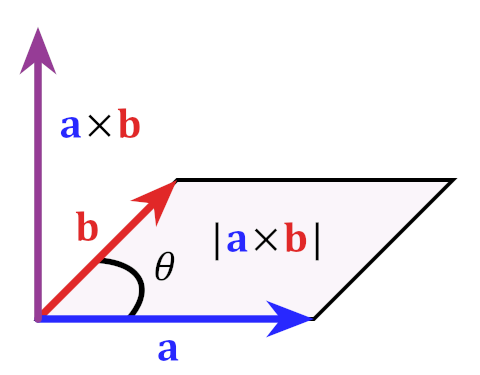
Figura a. Produto vetorial entre dois vetores a e b, resultando em um vetor perpendicular ao plano formado por a e b. A magnitude do produto vetorial (|a x b|) é igual à área do paralelogramo formado por a e b.

Cálculo do Produto Vetorial

O produto vetorial pode ser calculado utilizando as componentes dos vetores em um sistema de coordenadas cartesianas. Se u = (u₁, u₂, u₃) e v = (v₁, v₂, v₃), então:

u x v = (u₂v₃ – u₃v₂, u₃v₁ – u₁v₃, u₁v₂ – u₂v₁)

Uma forma prática de calcular o produto vetorial é utilizando o determinante de uma matriz:

onde i, j e k são os vetores unitários nas direções x, y e z, respectivamente.

Aplicações

O produto vetorial possui diversas aplicações, incluindo:

• Cálculo do torque: O torque τ exercido por uma força F em relação a um ponto é dado por:
  τ = r x F, onde r é o vetor que liga o ponto à linha de ação da força.
• Cálculo da área de um paralelogramo: A área do paralelogramo formado por dois vetores u e v é dada por |u x v|.
• Cálculo do momento angular: O momento angular L de uma partícula em relação a um ponto é dado por: L = r x p,  onde r é o vetor que liga o ponto à partícula e p é o momento linear da partícula.

Exercícios

1. Calcule o produto vetorial entre os vetores u = (1, 2, 3) e v = (-1, 0, 2).
2. Determine a área do paralelogramo formado pelos vetores u = (2, 1, 0) e v = (1, -1, 1).
3. Calcule o torque exercido por uma força F = (0, 10, 0) em relação à origem, sabendo que o ponto de aplicação da força é r = (2, 0, 0).