A representação gráfica de vetores é feita no plano cartesiano ou no espaço tridimensional, sendo uma ferramenta intuitiva para visualizar e entender suas características. Para representar um vetor de maneira gráfica, utilizamos as seguintes convenções:

• Origem: O ponto inicial do vetor. Em um sistema de coordenadas, normalmente é o ponto O(0,0) ou a origem do sistema.
• Ponta: O ponto final do vetor, que é determinado pela direção e pelo módulo do vetor.
• Seta: A seta no final do vetor indica a direção e o sentido da grandeza que ele representa.

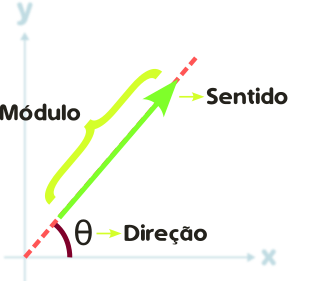
Figura a. Representação gráfica de um vetor, mostrando seus componentes essenciais: origem, ponta e seta indicativa de direção e sentido.

Características Gráficas de um Vetor

• Módulo (ou comprimento): O comprimento da seta do vetor indica o módulo. Em gráficos, o módulo é geralmente representado pela distância entre a origem e a ponta do vetor.
• Direção: A direção do vetor é dada pela linha reta que passa pela origem e pela ponta do vetor, representando a reta sobre a qual o vetor se encontra.
• Sentido: O sentido é indicado pela seta no final do vetor, mostrando para onde o vetor aponta ao longo da direção.

Fibura b. No plano cartesiano bidimensional, um vetor pode ser representado com as coordenadas da ponta a partir da origem.

Representação Algébrica de Vetores

A representação algébrica de vetores usa componentes numéricas para descrever as coordenadas de um vetor no espaço. Em um sistema de coordenadas cartesianas, um vetor é representado por suas componentes, que são os valores correspondentes às direções dos eixos.

• Vetores no Plano (2D)

No plano cartesiano bidimensional, um vetor v com origem na origem O(0, 0) e ponto final P(x, y) é representado como:

v = (x, y)

onde x e y são as componentes do vetor ao longo dos eixos X e Y, respectivamente.

Exemplo: Se um vetor v tem uma componente x = 3 e uma componente y = 4, sua representação algébrica será:

v = (3, 4)

• Vetores no Espaço (3D)

No espaço tridimensional, um vetor v é descrito por suas componentes ao longo dos eixos X, Y e Z:

v = (x, y, z)

onde x, y e z são as componentes ao longo dos eixos X, Y e Z, respectivamente.

Operações com Vetores

Com as representações algébrica e gráfica, podemos realizar diversas operações com vetores, como soma, subtração, multiplicação por escalar e cálculo do produto escalar. A seguir, destacamos algumas dessas operações:

• Soma de Vetores: Dois vetores a = (a₁, a₂) e b = (b₁, b₂) no plano podem ser somados componente a componente:

a + b = (a₁ + b₁, a₂ + b₂)

• Multiplicação de Vetor por Escalar: Se k é um escalar, a multiplicação do vetor v = (x, y) por k resulta no vetor:

k*v = (k*x, k*y)

• Produto Escalar: O produto escalar entre dois vetores a = (a₁, a₂) e b = (b₁, b₂) é dado por:

a · b = a₁ * b₁ + a₂ * b₂

Vantagens e Aplicações

A representação gráfica e algébrica de vetores tem várias aplicações em áreas como física, engenharia e computação. Por exemplo:

• Física: Em mecânica, vetores são usados para representar forças, velocidades e acelerações, entre outras grandezas vetoriais.
• Computação Gráfica: Na computação gráfica, vetores são essenciais para representar imagens, movimentos e orientações no espaço tridimensional.
• Engenharia: No estudo de estruturas, vetores são usados para modelar tensões, deslocamentos e fluxos.